The Error in the Comparator
Or, scikit-learn’s importance weighting in CV is broken.
Introduction
If the title doesn’t immediately give you chills, it should. Allow me to explain.
Defining what is meant by comparator is important. By comparator, I mean a total ordering on a set. Different programming languages call this binary relation by different names: Java calls it a Comparator, Scala an Ordering, Haskell calls it Ord and python admits a key function to establish order. Hopefully, the utility of such a comparison function is apparent. It establishes order on the elements of a set of objects. It enables operations like sorting, min and max.
But what happens if there’s a bug in this comparison function? Since its implementation is decoupled from the functions utilizing it, the correctness of the comparison function is independent of the algorithms (like sort, min and max) utilizing it. Even though the sort, min or max algorithms may be correct, using a buggy comparison function may give undesirable and wildly inaccurate results. This should not be surprising, but it should nonetheless be noted.
scikit-learn optimizes algorithm hyper-parameters during cross validation without considering importance weights in the metric computations used as a basis for comparing hyper-parameter configurations. Because models are trained with importance weights but not tested using importance weights, they are trained on a different distribution than the one used during validation. [4] shows that different hyper-parameters can indeed be returned when importance weighting is considered during metric calculations in cross validation.
Problem Description
While attempting to use importance weighting in a particular problem setting, I noticed that the metrics reported in
scikit-learn’s
cross validation routine seemed odd. I dug into the
issue and slowly started realizing that while importance weighting
has been available in the metric calculations themselves since 2014
(PR 3098 and
PR 3401), the sample_weight parameter in the metrics isn’t
being populated from the cross validation routines (see
_validation.py and
_search.py).
Consequently, hyper-parameter optimization
routines
like GridSearchCV and
RandomizedSearchCV
are also affected. Once I discovered this, I confirmed that sample_weight is properly propagated during model
training. The takeaway is this:
During cross validation in scikit-learn, importance weighting is used in model training but not validation.
To fully understand why this is an issue, it helps to understand why importance weighting is typically used. Wikipedia tells us:
“In statistics, importance sampling is a general technique for estimating properties of a particular distribution, while only having samples generated from a different distribution than the distribution of interest.” —https://en.wikipedia.org/wiki/Importance_sampling
It is typical that, during the (training) data generation phase of a modeling process, the sample distribution used in training is not representative of the population to which a learned model will be applied. This is a form of sampling bias that can have a detrimental effect when assessing model quality:
“In statistics, sampling bias is a bias in which a sample is collected in such a way that some members of the intended population are less likely to be included than others. It results in a biased sample, a non-random sample of a population (or non-human factors) in which all individuals, or instances, were not equally likely to have been selected. If this is not accounted for, results can be erroneously attributed to the phenomenon under study rather than to the method of sampling.” —https://en.wikipedia.org/wiki/Sampling_bias
We can start to see the problem take shape. When trying to address statistical issues like sampling bias, importance weighting can be used to unwind these biases introduced in the sampling process. This is predicated on the idea that importance weighting is consistently applied during training and validation. The fact that scikit-learn incorporates importance weights in training but not validation during cross validation means that models learn a distribution different than the one used to measure their efficacy. This is a manifestation of the same problem we sought to eliminate with importance weighting in the first place. See the rub? What is most consequential is that this problem appears inside the code that helps to sort (or rank) models in relation to their efficacy. To start to understand the issue more thoroughly, we’ll have to look at the definition of cross validation. \(\newcommand{\vect}[1]{\boldsymbol{#1}} \DeclareMathOperator*{\argmin}{\arg\!\min}\)
Cross Validation
Assume we have a training set \(\mathcal{T} = {\{ \left( x_{i}, y_{i} \right) \}}_{i=1}^{n}\) of size \(n\), split into \(k\) disjoint non-empty subsets, \({\{ \mathcal{T}_{i} \}}_{i=1}^{k}\). Given parameters \(\theta \in \Theta\), let \({ \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }\) be a function trained on \({\{ \mathcal{T}_{i} \}}_{i \ne j}\) and validated on test fold, \({ \mathcal{T} }_{ j }\). Then, given a loss function, \(\ell\), we can formally define \(k\)-fold cross validation as:
\[\frac { 1 }{ k } \sum _{ j=1 }^{ k }{ \frac { 1 }{ \left| { \mathcal{T} }_{ j } \right| } \sum _{ \left( x, y \right) \in { \mathcal{T} }_{ j } }{ \ell \left( x, y, { \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }\left( x \right) \right) } } \label{eq1}\tag{1}\]This is very similar to the definition found in [1] with the addition of the parameters, \(\theta\). The inner summation (and normalizing constant) describes the average loss within a test fold and the outer summation describes averaging over the test folds. Notice that the average loss within a test fold is bounded by the minimum and maximum loss of any \(\left( x, y \right) \in \mathcal{T}_{ j }\). Notice additionally that with this formulation, the average loss of each test fold has the same contribution in the outer summation, regardless of fold size.
Abstracting Cross Validation
We can abstract equation \(\left( \ref{eq1} \right)\) by replacing the within-fold average loss with a more general scoring function \(s \left( { \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }, \vect{x}_{\mathcal{T}_{ j }}, \vect{y}_{\mathcal{T}_{ j }} \right) \in \mathbb{R}\), where \(\vect{x}_{\mathcal{T}_{ j }}\) and \(\vect{y}_{\mathcal{T}_{ j }}\) are vectors of \(x\) and \(y\) values in \(\mathcal{T}_{ j }\), respectively. Assume that the magnitude of \(s\) is invariant to \(\left| { \mathcal{T} }_{ j } \right|\). This assumption is analogous to property in equation \(\left( \ref{eq1} \right)\) that the within-fold average loss is bounded by the minimum and maximum loss of any \(\left( x, y \right) \in \mathcal{T}_{ j }\), and is a generalization of the within-fold averaging. With these constraints, equation \(\left( \ref{eq1} \right)\) can then be rewritten as:
\[\frac { 1 }{ k } \sum _{ j=1 }^{ k }{ s \left( { \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }, \vect{x}_{\mathcal{T}_{ j }}, \vect{y}_{\mathcal{T}_{ j }} \right) } \label{eq2}\tag{2}\]If we loosen the constraint that each test fold \(j\) contributes equally to the global average (i.e., \(\forall{j} \in \left\{ 1, \ldots, k \right\}, w_{j} = \frac{1}{k}\))—thereby making the outer summation a weighted average—then equation \(\left( \ref{eq2} \right)\) can be rewritten as:
\[\frac{ \sum _{ j=1 }^{ k }{ w_{j} s \left( { \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }, \vect{x}_{\mathcal{T}_{ j }}, \vect{y}_{\mathcal{T}_{ j }} \right) } }{ \sum _{ j=1 }^{ k }{ w_{j} } } \label{eq3}\tag{3}\]Introducing Importance Weights into CV
To introduce importance weights into cross validation, \(\mathcal{T}_{ j }\) can be extended to include an importance weight vector, \(\vect{w}_{\mathcal{T}_{ j }} \in \mathbb{R}_{\ge 0}^{\left| \mathcal{T}_{ j } \right|}\), with the same indices in \(\vect{x}_{\mathcal{T}_{ j }}\) and \(\vect{y}_{\mathcal{T}_{ j }}\). The scoring function, \(s\), is also extended to accept the importance weights: \(s \left( { \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }, \vect{x}_{\mathcal{T}_{ j }}, \vect{y}_{\mathcal{T}_{ j }}, \vect{w}_{\mathcal{T}_{ j }} \right)\). Then equation \(\left( \ref{eq3} \right)\) becomes:
\[\frac{ \sum _{ j=1 }^{ k }{ w_{j} s \left( { \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }, \vect{x}_{\mathcal{T}_{ j }}, \vect{y}_{\mathcal{T}_{ j }}, \vect{w}_{\mathcal{T}_{ j }} \right) } }{ \sum _{ j=1 }^{ k }{ w_{j} } } \label{eq4}\tag{4}\]If we let \(w_{j} = \left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1}\), then \(\left( \ref{eq4} \right)\) can be rewritten as:
\[\frac{ \sum _{ j=1 }^{ k }{ \left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1} s \left( { \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }, \vect{x}_{\mathcal{T}_{ j }}, \vect{y}_{\mathcal{T}_{ j }}, \vect{w}_{\mathcal{T}_{ j }} \right) } }{ \sum _{ j=1 }^{ k }{ \left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1} } } \label{eq5}\tag{5}\]When I explained this to one of my colleagues, he was uneasy about the use of \(\vect{w}_{\mathcal{T}_{ j } }\) both inside \(s\) and in the mixing weight \(w_{j}\). Looking at \(\left( \ref{eq5} \right)\), his concern made sense to me. I realized that if \(\vect{w}_{\mathcal{T}_{ j } }\) was normalized (by the \(L_{1}\) norm), and it did not affect the results, then \(\left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1}\) would only be taken into account once in the importance weighted cross validation estimate. So I considered whether this was currently the case in scikit-learn and realized that all scoring functions that accept importance weights are invariant to \(\left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1}\). This can be seen in the interactive proof that I wrote with hypothesis. The proof can be found in [2]. After verifying the importance weight scale invariance of the built-in scoring functions in scikit-learn, I concluded that the final cross validation equation should be:
\[\frac{ \sum _{ j=1 }^{ k }{ \left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1} s \left( { \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }, \vect{x}_{\mathcal{T}_{ j }}, \vect{y}_{\mathcal{T}_{ j }}, \frac{ \vect{w}_{\mathcal{T}_{ j }} }{\left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1}} \right) } }{ \sum _{ j=1 }^{ k }{ \left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1} } } \label{eq6}\tag{6}\]In the case that the scoring function \(s\) is invariant to \(\left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1}\), then \(\left( \ref{eq5} \right)\) and \(\left( \ref{eq6} \right)\) are equivalent.
Test Results
To verify the behavior of importance weighted cross validation, I devised the following unit test.
This unit test looks at a few different scoring functions and some different importance weight vectors, but there are
always two folds and two examples per fold. The sample_weight vector is split into two folds, where the first two
values represent the first fold and the second two values represent the second fold. The bold-faced values represent
the weight associated with the single positive example in the fold and the non-bold faced values represent the weight
associated with the single negative example in the fold.
| Desired | scikit-learn | scoring fn | sample_weight |
|---|---|---|---|
| 0.999999 | 0.5 | accuracy | [1, 999999, 1, 999999] |
| 0.66666666 | 0.5 | accuracy | [100000, 200000, 100000, 200000] |
| 0.5 | 0.5 | accuracy | [100000, 100000, 100000, 100000] |
| 0.66666666 | 0.5 | accuracy | [200000, 100000, 200000, 100000] |
| 0.999999 | 0.5 | accuracy | [999999, 1, 999999, 1] |
| 0.25000025 | 0.5 | accuracy | [2000000, 1000000, 1, 999999] |
| 2.5 x 10-7 | 0.25 | precision | [2000000, 1000000, 1, 999999] |
| -0.5389724 | -0.8695388 | log loss | [2500000, 500000, 200000, 100000] |
| -0.1742424 | -0.3194442 | Brier score | [2500000, 500000, 200000, 100000] |
Since scikit-learn does not incorporate importance weights, the results are rather undesirable. For instance, the accuracy value is always 0.5 since it only correctly classifies one example per fold (but disregards importance). If instead of importance weights, the data was replicated the number of times indicated by the importance weights, then scikit-learn’s results would align with the desired importance weighted results if the size of the two folds are equal. If data replication rather than importance weighting was employed and scikit-learn used weighted averaging across folds on the relative test fold sizes rather than simple averaging, then scikit-learn’s results would align with the desired results.
The need for weighted averaging can be seen when observing the behavior of leave-one-out cross validation. Since
the scoring functions are invariant to the \(L_{1}\) norm of the sample_weight vector, importance weighted cross
validation cannot work without weighted averaging across folds. It would simply be regular unweighted leave-one-out
cross validation.
It is obvious from the Table 1, but it should be noted that the scikit-learn’s cross validation metrics can under or over predict the importance weighted estimate, sometimes rather dramatically.
One should pay extra close attention to the example with weights \(\left[ 2000000, 1000000, 1, 999999\right]^T\) and the accuracy metric. Notice that the cross validation estimate is:
\[0.25000025 = \frac{1000001}{4000000} = \left( 1 - \frac{2000000}{3000000} \right) \frac{3000000}{4000000} + \frac{1}{1000000} \frac{1000000}{4000000}\]If the sample_weight vector were instead \(\left[ 200, 100, 1, 99\right]^T\), the accuracy estimate becomes
0.2525. To bolster the claim that weighted averaging offers better estimates than simple averaging when combining
the within-fold estimates, we can calculate the expected accuracy when there is a population of 400 examples with
201 positive examples. Using 201 positives of 400 examples and allowing the examples to fall into any fold
allows us to calculate the expected accuracy over all possible fold combinations. This can be calculated using the
hypergeometric distribution. See [3] for
details. The expected accuracy results in the following graph where accuracy varies with the fold sizes.
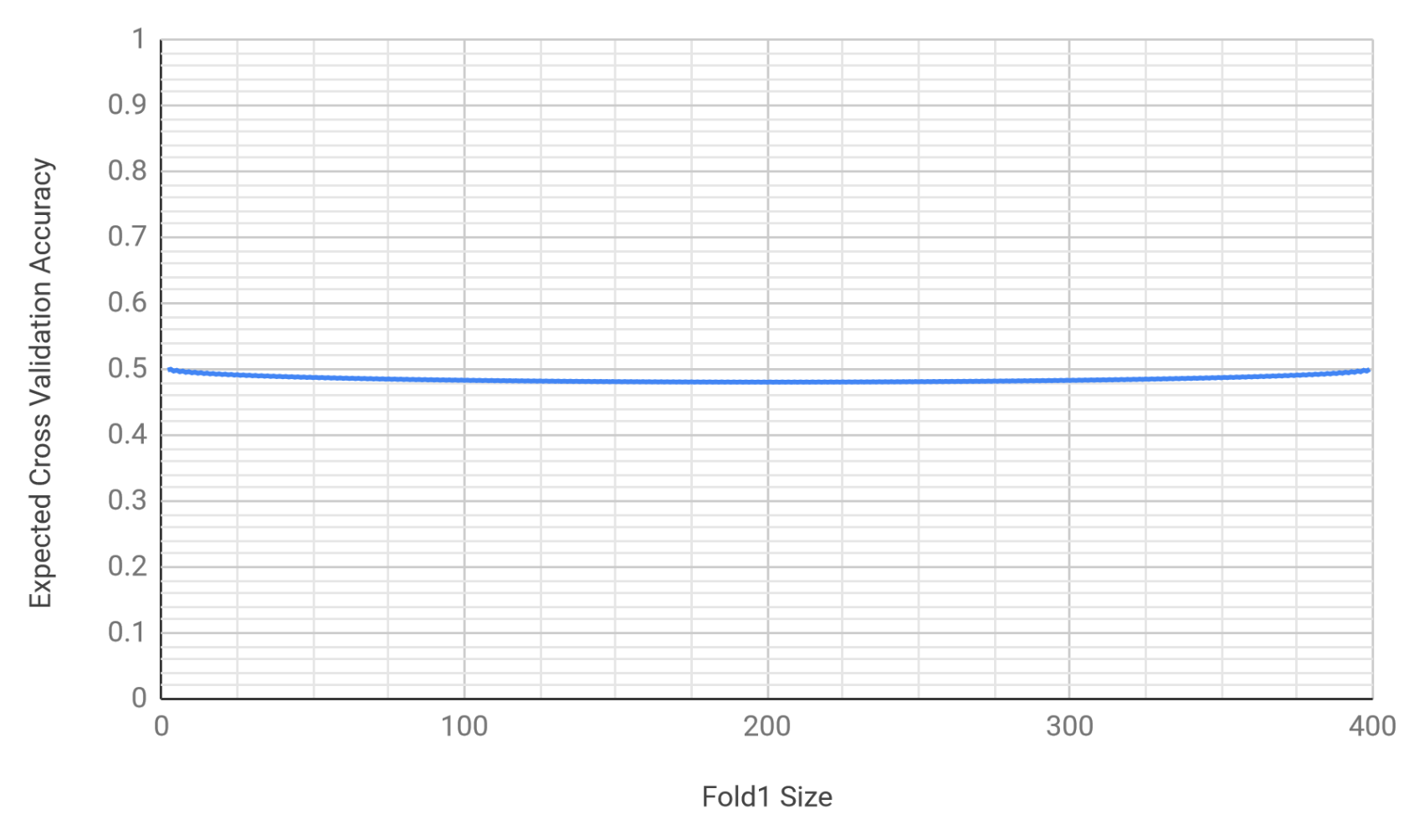
This graph shows that the expected accuracy lies in the interval \(\left[ 0.48029, 0.50003 \right]\); where in the interval depends on the fold sizes. If simple averaging were used, the 2-fold cross validation estimate would be:
\[0.171666 = \frac{103}{600} = \left( 1 - \frac{200}{300} \right) \frac{1}{2} + \frac{1}{100} \frac{1}{2}\]which is directionally incorrect versus 0.2525 in relation to the above interval.
“The Error in the Comparator” Revisited
Finally, the punchline: the reason I deem this problem the “Error in the Comparator” is that as we’ve seen, the cross validation estimates in scikit-learn are not really in line with what one should expect. The results using importance weighting with integer weights should be the same as performing cross validation with replicated data, but they are not the same under scikit-learn. This is rather disconcerting. When cross validation is used in hyper-parameter search, the cross validation estimates are used as a basis of comparison from which the “optimal” values in the hyper-parameter space are selected. This can be seen in the following equation that codifies hyper-parameter search, where \(\theta\) represents a hyper-parameter setting in the hyper-parameter space, \(\Theta\):
\[\widehat{\theta} = \argmin_{\theta \in \Theta}{ \frac{ \sum _{ j=1 }^{ k }{ \left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1} s \left( { \widehat { f } }_{ \theta, { \mathcal{T} }_{ j } }, \vect{x}_{\mathcal{T}_{ j }}, \vect{y}_{\mathcal{T}_{ j }}, \frac{ \vect{w}_{\mathcal{T}_{ j }} }{\left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1}} \right) } }{ \sum _{ j=1 }^{ k }{ \left \lVert { \vect{w}_{\mathcal{T}_{ j } } } \right \rVert _{1} } } } \label{eq7}\tag{7}\]Discussion
This issue has bean present in scikit-learn since 2015. Multiple open tickets have been on GitHub since April 2015. Issue 4632 (April 24, 2015) asks “should cross-validation scoring take sample-weights into account?” Issue 4497 (April 2, 2015) is concerned with API consistency and naming issues. What, in my opinion, is so appalling about this is that these issues have been open for nearly four years! It seems that these tickets have been bogged down in naming conventions and API consistency and meanwhile, this issue has silently crept into many codebases. scikit-learn has very wide adoption. The testimonials page lists leading financial institutions as well as prominent tech companies as adopters. Now, let me pose the question: if you are investing money with a financial institution that uses scikit-learn for financial modeling, would you not want hyper-parameter search to use the training distribution as the basis for selecting hyper-parameters in those financial models? if you have ever complained about music recommendation algorithms, would you not want a company invested in making music recommendations to use the same distribution for training and model validation? This is the scope of this problem. It is a big problem! Arguments about naming conventions are not an appropriate excuse for letting this issue fall through the cracks.
The biggest problem that I see is that this issue has for years been a known problem (and there have been pull requests to attempt to fix this), but people have been so apathetic that these fixes solutions have not really been considered. See the GitHub issues listed above for more context. Meanwhile, there is no indication that the problem is actually occurring, save scrutinizing the results. No warnings are emitted, no errors raised or exceptions thrown: nothing.
On a personal note, it took me over an hour and a half of pair programming and debugging into the scikit-learn code in order to convince one of my colleagues that this issue existed at all. The reason it was so difficult to convince him was that he was incredulous due to the fact that he had previously used importance weighted cross validation in scikit-learn. Since the cross validation code did not result in any kind of error, he was oblivious to problem and had no reason to question the validity of the results. This is exactly the danger I am trying to warn against here: a problem arising due to our willingness to implicitly trust testing and validation code.
Pull Requests
I fixed this issue in internal forks but this issue deserves real consideration. This problem needs to be addressed with the gravity it is due. I have created pull requests for both scikit-learn (https://github.com/scikit-learn/scikit-learn/pull/13432) and a distributed version for dask (https://github.com/dask/dask-ml/pull/481) in the hope that this will benefit others. I created this post to point out the problem and its gravity along with a viable fix. Please give this issue the importance it deserves.
(Part II will further discuss [1].)
Author’s Note
There may be nothing especially novel in this article. There are no proofs of correctness, merely evidence in the form of tests supporting the existence of flaws in the cross validation routines in scikit-learn.
License
The above code is released under the MIT License, Copyright (c) 2019 Ryan Deak.
References
- Sugiyama, Masashi, Matthias Krauledat, and Klaus-Robert Muller. “Covariate shift adaptation by importance weighted cross validation.” Journal of Machine Learning Research 8. May (2007): 985-1005.
- Deak, Ryan. “sklearn_scorer_wt_invariant.py” Gist, https://gist.github.com/deaktator/94545f807f139eba2c8a15381f2495e0. Accessed 5 Mar. 2019.
- Deak, Ryan. “hypergeom_sklearn_imp_wt.py” Gist, https://gist.github.com/deaktator/1080eca4c291070d009014f2f2d759ad Accessed 5 Mar. 2019.
- Deak, Ryan. “wt_cv_eval_is_diff_unwt_cv.py” Gist, https://gist.github.com/deaktator/644086d0093b94fab567388f8008fe19