Optimizing Pairs of Like Things

An interesting task is to take a group of items and pair the items together. This is especially interesting when a value can be assigned to each pair and the items are not infinitely replicable. Given this setting, we might want to find the set of pairs that optimizes the total additive value of the pairs of items.

In the event that the items can be partitioned into two sets, we have a bipartite graph for which many variants of the above scenario exist:

1. Assignment Problem
2. Transportation Problem
3. Maximal Matching
4. Baseball Elimination

Non-bipartite pairing optimization

Ordered pairs, separate capacities

But what about more general, non-bipartite problems? Let’s start with the problem of finding the set of pairs that optimize the total additive value of the pairs when:

1. Order in the pair matters, i.e. \((u, v) \neq (v, u)\)
2. Replication of items depends on whether the item occurs on the left or right of a pair.

This is rather easy because it actually decomposes to bipartite graph problem. We can create a bipartite graph where items that can appear on the left of a pair are in the left group of the graph and similarly, items that can appear on the right are in the right group. Note that the Left (\(L\)) and Right (\(R\)) groups are not necessarily mutually exclusive, i.e. \(\left| L\bigcap R \right| \ge 0\). In this case, we create a single source, single sink min cost max flow problem. The capacities on the arcs from the source to a node indicate the number of times the item can appear on the left side of a pair. Similarly, the capacities on arcs from a node to the sink indicate the number of times the item can appear on the right side of a pair. These nodes should be 0 cost arcs. The arcs between two items \(u \in L\) and \(v \in R\) indicate that the pair \((u, v)\) could be made. The capacity of these arcs is one and the cost assigned to these arcs is minimized. Maximizing the sum of positive rewards can be accomplished by minimizing the sum of negative rewards.

Mathematical formulation

A graphical example

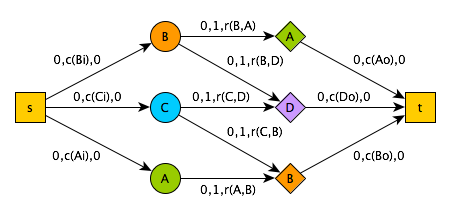
Here square nodes represent the source and sink, circular nodes represent items that can appear first in the pair and diamonds nodes are represent items that can appear second in the pair. The 3-tuples are (minimum capacity, maximum capacity, reward per unit flow). The goal is to maximize the reward across the entire network.

2-Item sets, one replication limit per item

If we don’t care about the order in which items appear in the pair, but disallow an item being paired with itself, then we have a few options. We can attempt to model the problem as an optimization problem on

1. an undirected graph OR
2. a directed graph

Since a bunch of solvers, such as CS2, exist for directed graphs, we’ll focus our efforts on modeling the problem as a min-cost max flow problem on a directed graph. The first thing we need to notice is that since we are not dealing with infinitely replicable items, we need to limit the number of times each item can appear in pairs that are created. Luckily, it’s possible to do so by a fairly well known transformation. The method is described in the Maximum flow problem with vertex capacities section on the Maximum flow problem wikipedia page.

Every potential pair of items \(u\) and \(v\) is modeled as an arc \((u, v)\) with an associated cost \(c\). Then we must limit the number of times the items can be used. This is accomplished by splitting each node representing an item, \(u\), into two nodes \({ u }_{ in }\) and \({ u }_{ out }\) and creating an arc \(\left( { u }_{ in }, { u }_{ out } \right)\) where the arc capacity is equal to the number of times item \(u\) can be included in a pair and unit cost 0. Then, for all potential pairs \(\left( u, v \right)\), we replace the arcs with \(\left( { u }_{ out }, { v }_{ in } \right)\).

Finally, we have to create arcs from the source and to the sink and then we can apply a standard min-cost max flow. For each arc \(\left( { u }_{ in }, { u }_{ out } \right)\) with capacity \(C\), we create two additional arcs \(\left( s, { u }_{ in } \right)\) and \(\left( { u }_{ out }, t \right)\), each with a capacity greater than or equal to \(C\) (\(\infty\) is okay) and unit cost 0. Here \(s\) and \(t\) represent the source node and sink node, respectively. Finally we create an arc \(\left( s, t \right)\) with capacity \(\infty\) and unit cost 0.

A detail left out of the above algorithm is the directionality of arcs. Directionality doesn’t matter since we are limiting the number of times each item can be used but there are a couple of ways to choose directionality:

1. Assign arcs direction randomly.
2. Assign IDs with a strict total order to each node and require that each directed arcs \(\left( u, v \right)\) exists only if \(u < v\).

A graphical example

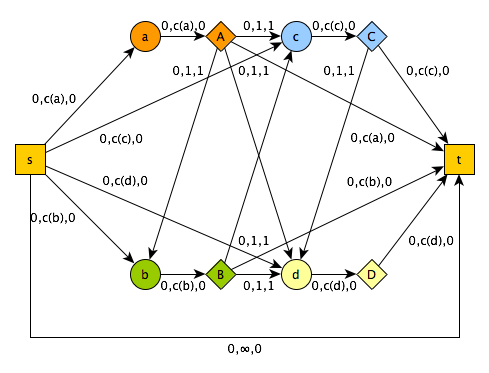
Here square nodes represent the source and sink, circular nodes are input nodes and diamonds nodes are output nodes. The 3-tuples are (minimum capacity, maximum capacity, reward per unit flow). The goal is to maximize the reward across the entire network.

A working DIMACS encoding of this problem can be found in the non-bipartite directory in my maxflow-problems github repo.

Number of nodes and arcs

This method requires:

• \(2 \lvert V \rvert + 2\) nodes
• \(\lvert E \rvert + 3 \lvert V \rvert + 1\) edges

where \(V\) is the set of items and \(E\) is the set of potential pairs.

Applications

This problem has a lot of applications but may be especially relevant in social networks where people are suggested to people with the intent of maximizing some global quantity in the network. This could also be used to maximize discounts on items that when purchased together on Amazon save money.

Extensions

We’ll look at how we can extend this solution in a future post but for a previous of some possible extensions, see the README on my maxflow-problems github repo.

References

• https://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/matching.pdf
• http://econweb.ucsd.edu/~jsobel/172aw02/notes8.pdf