Bag of words, or word count, is a very parallelizable algorithm and is one of the canonical examples in both Hadoop and Spark, so much so that it is on the Spark landing page.

While I was working on an Aloha bug related to skip grams, I wanted to do some simple benchmarking via Google Caliper to make sure to use the right implementations. I’m not concerned about large-scale map-reduce implementations, but performant single-box ones. Since Aloha is used at eHarmony in a lot of scoring applications, it’s possible that this implementation could be used billions (109+) of times per day. So shaving a millisecond could make a HUGE difference. I tested 8 variants against each other. The implementations can be found in my skip-grams-bench project.

Variants

  1. bagOfWords1: Iterate over tokens in parallel and update counts in a mutable concurrent AtomicInteger TrieMap.
  2. bagOfWords2: Immutable, not parallel. groupBy followed by mapValues(_.size).
  3. bagOfWords3: Iterate over tokens (not parallel) and update counts in a mutable map of Int.
  4. skipGrams1: Skipgram algorithm using parallel token range that update counts in a mutable concurrent AtomicInteger TrieMap.
  5. skipGrams2: Skipgram algorithm that splits the token range into one chunk per thread and then iterate each chunk in parallel. Update counts in a mutable concurrent AtomicInteger TrieMap.
  6. skipGrams3: like skipGrams1 but uses a fold-left instead of a while loop as the innermost loop.
  7. skipGrams4: A non-parallel variant of skipGrams1. Uses a mutable map of Int.
  8. skipGrams5: A non-parallel variant of skipGrams3. Uses a mutable map of Int.

Data Collected

Using the default benchmarks settings in Caliper gives three main measures:

  1. Runtime
  2. Memory usage
  3. Object allocations

The string used for testing was a substring of π. The nine different string lengths tested were 2k for k = 5,…,9 and 10k for k = 3,…,6. The splitting criterion was different digits, 1 – 9.

Data was collected on my desktop with a 6-core Core i7-3930K CPU.

Charts

Runtime

Let’s look at runtime first. The first scatter plot shows the overall picture. Notice that the for small string sizes, non-parallel algorithms dominate. We can see bagOfWords3, skipGrams5, and bagOfWords2 dominate on string sizes up to 1,000 or so. Then at lengths of 10,000 we start to see the picture change and parallel algorithms start to take over.

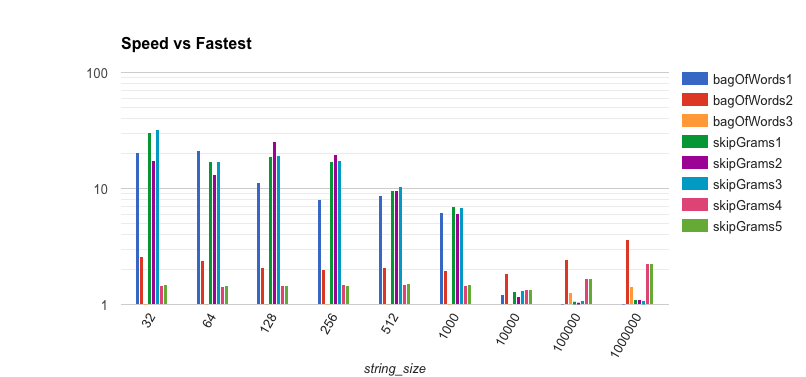
Runtime (sec)

We need to drill down and see what’s going on, so I first looked at the log plot of the runtimes versus the fastest algorithm for the string size. What we see is rather remarkable. The parallel algorithms are an order of magnitude or more slower for smaller strings (up to 128), and they still remain almost an order of magnitude slower for mid-length strings (up to 512). Then at 10,000 we see a completely different picture. All of the parallel algorithms keep up with each other and you can see the trend of the gap growing larger between 10,000 and 1,000,000. At 1,000,000, all but these fastest non-parallel algorithms are at least twice as slow.

Runtime (sec)

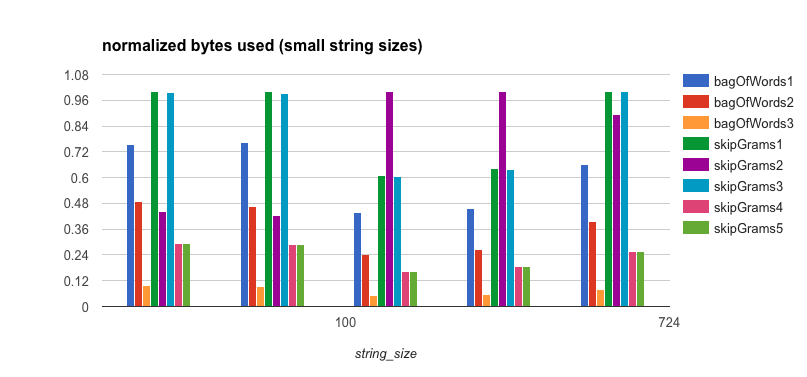
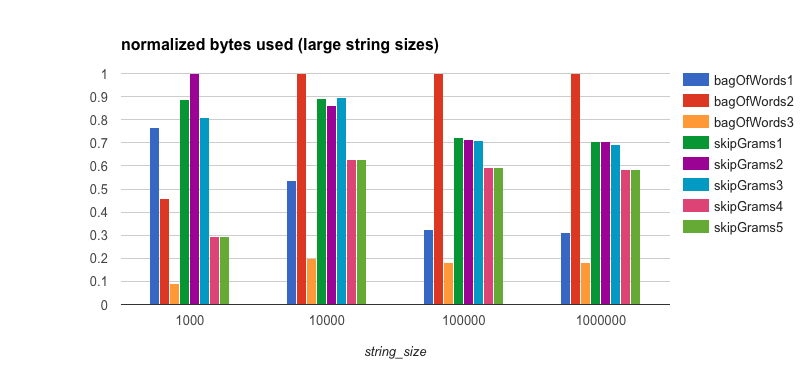
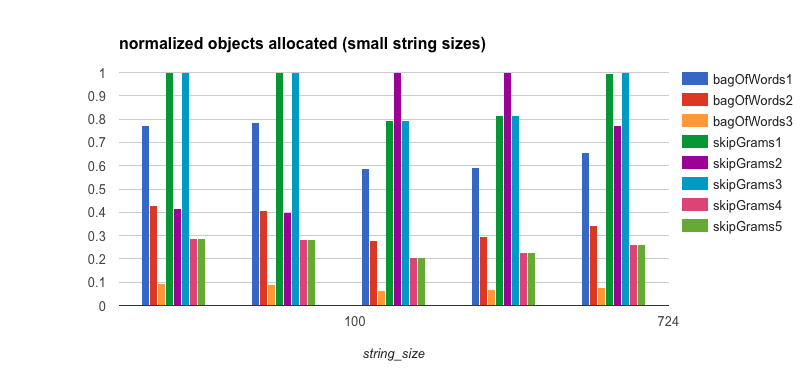
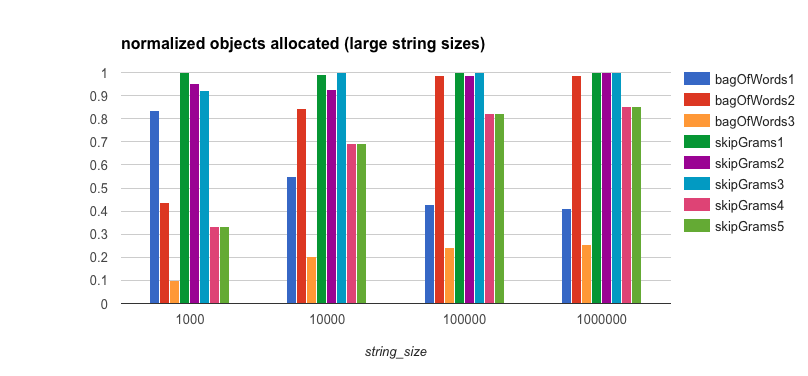
Memory and Object Allocation

It’s clear that the reason the bagOfWords3 algorithm does so well, even though it’s not parallelized, is that it has much lower overhead from both a memory and object allocation standpoint. Therefore, it will be easier on the garbage collector in the JVM. This is also the case for bagOfWords1, albeit to a lesser extent than in bagOfWords3. This is because of the thread-safe TrieMap implementation that is used and that the values are AtomicIntegers rather than plain integers.

Bytes allocated (small string)

Bytes allocated (large string)

Objects allocated (small string)

Objects allocated (large string)

Conclusions

Use a simple, non-parallel, mutable bag of words implementation for small strings. For larger strings, it’s not so clear other than parallelizing is worth it. Using a general purpose parallelized skipgrams implementation is about 10% slower, so if speed really matters, use a specialized parallel bag of words implementation. Otherwise, just pass 0 for skips and 1 for gram size to the skipgrams algorithm, and you’re done.

Caliper Benchmark

Caliper results are available here.

Code

Code is available at https://github.com/deaktator/skip-grams-bench under the MIT License.